কম্পিউটারের নম্বর ব্যবস্থা
তথ্য কণিকা
- যে পদ্ধতিতে সংখ্যা গণনা করা হয় বা প্রকাশ করা হয়, তাকে বলে- সংখ্যা পদ্ধতি।
- সংখ্যা পদ্ধতিকে সাধারণত ভাগ করা হয়- চারভাগে।
- সংখ্যা পদ্ধতিগুলো হলো- ডেসিমাল বা দশমিক সংখ্যা পদ্ধতি, বাইনারি সংখ্যা পদ্ধতি, অক্টাল সংখ্যা পদ্ধতি ও হেক্সাডেসিমাল সংখ্যা পদ্ধতি।
- দশমিক সংখ্যা পদ্ধতির ভিত্তি হচ্ছে- ১০।
- দশমিক সংখ্যা পদ্ধতিতে প্রতীক হলো- দশটি (০, ১, ২, ৩, ৪, ৫, ৬, ৭, ৮, ৯)।
- কোনো সার্থক অঙ্ক আলাদাভাবে লিখলে যে সংখ্যা প্রকাশ করে, তা হলো- অঙ্কের স্বকীয় মান।
- বাইনারি সংখ্যার ভিত্তি হলো- ২।
- বাইনারি সংখ্যা পদ্ধতিতে প্রতীক হলো- দুটি; যথা: ০ ও ১।
- কম্পিউটারে ডেটা সংরক্ষণের জন্য ব্যবহার করা হয়- বাইনারি (Binary) সংখ্যা পদ্ধতি।
- কয়েকটি অঙ্ক পাশাপাশি লিখলে কোনো সার্থক অঙ্ক তার অবস্থানের জন্য যে সংখ্যা প্রকাশ করে তাকে বলে- ঐ অঙ্কের স্থানীয় মান।
- কম্পিউটার গাণিতিক কার্যাবলী (Mathematical function) সম্পাদন করে- Binary সংখ্যা পদ্ধতি ব্যবহার করে।
- কম্পিউটারে সমস্ত কাজ সম্পাদিত হয়- ০ ও ১ ব্যবহার করে।
- ডিজিটাল সিস্টেমে ১ মানে- on/true/high/active
- ডিজিটাল সিস্টেমে ০ মানে- off/false/low/inactive
- Analog সংকেত (যেমন- text, code ইত্যাদি) কম্পিউটারে রূপান্তরিত হয়- Binary Format-এ।
- কম্পিউটারে ডিজিটাল পদ্ধতি হলো- বাইনারি (Binary)।
- বিদ্যুতের উপস্থিতি ও অনুপস্থিতির উপর নির্ভরশীল- কম্পিউটার প্রযুক্তি।
- যে সংখ্যা পদ্ধতিতে আটটি অঙ্ক বা চিহ্ন ব্যবহার করা হয় তাকে বলে- অক্টাল সংখ্যা পদ্ধতি।
- অক্টাল সংখ্যা পদ্ধতির ভিত্তি হচ্ছে- ৮।
- অক্টাল সংখ্যা পদ্ধতিতে ব্যবহৃত অঙ্ক ৮টি হলো- ০, ১, ২, ৩, ৪, ৫, ৬, ৭।
- যে সংখ্যা পদ্ধতিতে ১৬টি অঙ্ক বা চিহ্ন ব্যবহার করা হয় তাকে বলে হেক্সাডেসিমাল পদ্ধতি।
- হেক্সাডেসিমাল সংখ্যা পদ্ধতির ভিত্তি হচ্ছে-১৬।
- হেক্সাডেসিমাল সংখ্যা পদ্ধতিতে ব্যবহৃত অঙ্ক ১৬টি হলো- ০, ১, ২, ৩, ৪, ৫, ৬, ৭, ৮, ৯, A, B, C, D, E, F
- হেক্সাডেসিমাল নম্বর গঠনের সংমিশ্রণ হলো- ডেসিমাল ডিজিট (০, ১, ২, ৩, ৪, ৫, ৬, ৭, ৮, ৯) ও অক্ষর (A, B, C, D, E, F)।
- প্রতিটি বর্ণ, অঙ্ক বা বিশেষ চিহ্নকে আলাদাভাবে সিপিইউকে নির্দেশ করার জন্য বিটের (০ বা ১) বিভিন্ন বিন্যাসের সাহায্যে অদ্বিতীয় সংকেত তৈরি করা হয়। এই অদ্বিতীয় সংকেতকে বলা হয়- কোড।
- ইলেকট্রনিক সিগন্যালকে বাইনারি ডিজিট ০ এবং ১-এ প্রকাশ করাই হলো-বিট।
- আটটি বিট নিয়ে গঠিত- একটি বাইট (অর্থাৎ ১ বাইট = ৮ বিট)।
- কম্পিউটার পদ্ধতিতে এক মেগাবাইট = (১০২৪ × ১০২৪) বাইট।
- কম্পিউটার পদ্ধতিতে এক গিগাবাইট = ১০২৪৩ বাইট।
- MSB-Most Significant Bit, LSB-Last Significant Bit.
দশমিক, বাইনারি, অক্টাল ও হেক্সাডেসিমাল সংখ্যার তুলনা ছক
| দশমিক | বাইনারি | অক্টাল | হেক্সাডেসিমাল |
|---|---|---|---|
| ০ | ০ | ০ | ০ |
| ১ | ১ | ১ | ১ |
| ২ | ১০ | ২ | ২ |
| ৩ | ১১ | ৩ | ৩ |
| ৪ | ১০০ | ৪ | ৪ |
| ৫ | ১০১ | ৫ | ৫ |
| ৬ | ১১০ | ৬ | ৬ |
| ৭ | ১১১ | ৭ | ৭ |
| ৮ | ১০০০ | ১০ | ৮ |
| ৯ | ১০০১ | ১১ | ৯ |
| ১০ | ১০১০ | ১২ | A |
| ১১ | ১০১১ | ১৩ | B |
| ১২ | ১১০০ | ১৪ | C |
| ১৩ | ১১০১ | ১৫ | D |
| ১৪ | ১১১০ | ১৬ | E |
| ১৫ | ১১১১ | ১৭ | F |
বিভিন্ন সংখ্যায় রূপান্তর
দশমিক সংখ্যা থেকে বাইনারি, অক্টাল ও হেক্সাডেসিমেল সংখ্যায় রূপান্তর
দশমিক সংখ্যা হতে বাইনারি সংখ্যায় রূপান্তর (Decimal to Binary)
দশমিক সংখ্যা হতে বাইনারি সংখ্যায় রূপান্তর করতে হলে দশমিক সংখ্যাকে ২ দ্বারা ভাগ করে প্রাপ্ত ভাগফলকে পুনরায় ২ দ্বারা ভাগ করতে হয়। এভাবে ততক্ষণ পর্যন্ত ভাগ করতে হবে যতক্ষণ পর্যন্ত না ভাগফল ০ হয়। এবার ভাগশেষগুলো বিপরীত দিক হতে পাশাপাশি লিখে দশমিক সংখ্যাটির সমকক্ষ বাইনারি সংখ্যা পাওয়া যাবে।
উদাহরণ: (২৩)১০-কে বাইনারিতে রূপান্তর করুন। সমাধান: অবশিষ্ট (Reminder)
\[ \begin{array}{c|c} \text{Quotient} & \text{Remainder} \\ \hline ২৩ \div ২ = ১১ & ১ \\ ১১ \div ২ = ৫ & ১ \\ ৫ \div ২ = ২ & ১ \\ ২ \div ২ = ১ & ০ \\ ১ \div ২ = ০ & ১ \\ \end{array} \]
\[ ২৩_{১০} = ১০১১১_২ \]
ভগ্নাংশের ক্ষেত্রে দশমিক হতে বাইনারিতে রূপান্তর
দশমিক ভগ্নাংশকে 2 দ্বারা গুণ করতে হয় এবং গুণফলের পূর্ণ অঙ্কটি আলাদা রেখে ভগ্নাংশ অঙ্কটিকে পুনরায় 2 দ্বারা গুণ করতে হয়, এভাবে ততক্ষণ পর্যন্ত গুণ করতে হয় যতক্ষণ পর্যন্ত না গুণফল ০ (শূন্য) হয়। বার বার গুণ করার পর যদি ০ (শূন্য) না আসে তবে পাঁচবার গুণ করলেই যথেষ্ট। এরপর পূর্ণ অঙ্ক হিসেবে প্রাপ্ত অঙ্কগুলো প্রাপ্তির ক্রমানুসারে পাশাপাশি লিখে দশমিক সংখ্যার সমকক্ষ বাইনারি সংখ্যা পাওয়া যায়।
উদাহরণ ১: (০.৪৬)১০ কে বাইনারিতে রূপান্তর করুন। সমাধান: \[ ০.৪৬_{১০} = ০.\overline{০১১১}_{২} \text{ (approx)} \] \[ ০.৪৬ \times ২ = ০.৯২ \quad \Rightarrow \quad \text{integer part} = ০ \] \[ ০.৯২ \times ২ = ১.৮৪ \quad \Rightarrow \quad \text{integer part} = ১ \] \[ ০.৮৪ \times ২ = ১.৬৮ \quad \Rightarrow \quad \text{integer part} = ১ \] \[ ০.৬৮ \times ২ = ১.৩৬ \quad \Rightarrow \quad \text{integer part} = ১ \] \[ ০.৩৬ \times ২ = ০.৭২ \quad \Rightarrow \quad \text{integer part} = ০ \] \[ ০.৭২ \times ২ = ১.৪৪ \quad \Rightarrow \quad \text{integer part} = ১ \] \[ ০.৪৪ \times ২ = ০.৮৮ \quad \Rightarrow \quad \text{integer part} = ০ \] \[ ০.৪৬_{১০} \approx ০.০১১১০১_{২} \]
উদাহরণ ২: (১২৩.৪৫) কে বাইনারিতে রূপান্তর করুন।
পূর্ন অংশ: \(১২৩_{১০} \to \text{Binary}\) \[ ১২৩ \div ২ = ৬১ \quad \text{remainder} = ১ \] \[ ৬১ \div ২ = ৩০ \quad \text{remainder} = ১ \] \[ ৩০ \div ২ = ১৫ \quad \text{remainder} = ০ \] \[ ১৫ \div ২ = ৭ \quad \text{remainder} = ১ \] \[ ৭ \div ২ = ৩ \quad \text{remainder} = ১ \] \[ ৩ \div ২ = ১ \quad \text{remainder} = ১ \] \[ ১ \div ২ = ০ \quad \text{remainder} = ১ \] \[ ১২৩_{১০} = ১১১১০১১_{২} \] ভগ্নাংশ অংশ \[ ০.৪৫ \times ২ = ০.৯০ \quad \Rightarrow \quad \text{integer part} = ০ \] \[ ০.৯০ \times ২ = ১.৮০ \quad \Rightarrow \quad \text{integer part} = ১ \] \[ ০.৮০ \times ২ = ১.৬০ \quad \Rightarrow \quad \text{integer part} = ০ \] \[ ০.৬০ \times ২ = ১.২০ \quad \Rightarrow \quad \text{integer part} = ১ \] \[ ০.২০ \times ২ = ০.৪০ \quad \Rightarrow \quad \text{integer part} = ০ \] \[ ০.৪০ \times ২ = ০.৮০ \quad \Rightarrow \quad \text{integer part} = ০ \] \[ ০.৮০ \times ২ = ১.৬০ \quad \Rightarrow \quad \text{integer part} = ১ \] \[ ০.৪৫_{১০} \approx 0.০১১১০০১_{২} \] \[ ১২৩.৪৫_{১০} \approx ১১১১০১১.০১১১০০১_{২} \]
দশমিক থেকে অক্টালে রূপান্তর
দশমিক সংখ্যাকে পর্যায়ক্রমে ৮ দিয়ে ভাগ করে ভাগশেষগুলোকে একত্র করে দশমিক সংখ্যাটির অক্টাল সমকক্ষ সংখ্যা পাওয়া যায়। প্রথম এবং শেষ ভাগশেষ দুটি সংখ্যাকে যথাক্রমে অক্টাল সংখ্যার সর্বনিম্ন ও সর্বোচ্চ গুরুত্বপূর্ণ স্থানে বসাতে হয়।
উদাহরণ: (২৩.১২৫)১০ কে অক্টালে রূপান্তর করুন।
পূর্ণ অংশের ক্ষেত্রে (৮ দ্বারা ভাগ) \[ ২৩ \div ৮ = ২ \quad \text{remainder} = ৭ \] \[ ২ \div ৮ = ০ \quad \text{remainder} = ২ \] \[ ২৩_{১০} = ২৭_{৮} \] ভগ্নাংশের ক্ষেত্রে (৮ দ্বারা গুণ): \[ ০.১২৫ \times ৮ = ১.০ \quad \Rightarrow \quad \text{integer part} = ১ \] \[ ০.১২৫_{১০} = ০.১_{৮} \] পুর্ণ অংশ এবং ভগ্নাংশ একত্র করেঃ \[ ২৩.১২৫_{১০} = ২৭.১_{৮} \]
দশমিক থেকে হেক্সাডেসিমেলে রূপান্তর
দশমিক থেকে হেক্সাডেসিমেলে রূপান্তরের প্রক্রিয়ায় দশমিক পূর্ণসংখ্যাকে পর্যায়ক্রমে ১৬ দ্বারা ভাগ এবং ভগ্নাংশকে ১৬ দ্বারা গুণ করতে হয়।
উদাহরণ: (৮৫০)১০ কে হেক্সাডেসিমেলে রূপান্তর করুন। \[ ৮৫০ \div ১৬ = ৫৩ \quad \text{remainder} = ২ \] \[ ৫৩ \div ১৬ = ৩ \quad \text{remainder} = ৫ \] \[ ৩ \div ১৬ = ০ \quad \text{remainder} = ৩ \] ভাগশেষগুলোকে নিচ থেকে উপরে সাজিয়ে লিখে: \[ ৮৫০_{১০} = ৩৫২_{১৬} \]
বাইনারি, অক্টাল ও হেক্সাডেসিমেল সংখ্যা হতে দশমিক সংখ্যায় রূপান্তর
যে কোনো সংখ্যা পদ্ধতি থেকে দশমিক সংখ্যা পদ্ধতিতে রূপান্তরের সাধারণ নিয়ম-
বাইনারি/অক্টাল/হেক্সাডেসিমেল অথবা অন্য কোনো সংখ্যা পদ্ধতি থেকে দশমিক সংখ্যা পদ্ধতিতে সংখ্যার রূপান্তরের ক্ষেত্রে নিম্নলিখিত ধাপগুলো অনুসরণ করতে হবে। উল্লেখ্য এ ক্ষেত্রে পূর্ণাঙ্গ এবং ভগ্নাংশের জন্য একই নিয়ম প্রযোজ্য।
ধাপ-১: প্রদত্ত সংখ্যাটির বেজ শনাক্ত করে সংখ্যাটির অর্ন্তগত প্রত্যেকটি অংকের স্থানীয় মান বের করতে হবে।
ধাপ-২: সংখ্যার অন্তর্গত প্রত্যেকটি অংকের নিজস্ব মানকে তার স্থানীয় মান দিয়ে গুণ করতে হবে।
ধাপ-৩: গুণফলগুলোর যোগফলই হবে সমতুল্য দশমিক সংখ্যা।
বাইনারি থেকে দশমিকে রূপান্তর
বাইনারি সংখ্যার প্রতিটি ১ এর স্থানীয় মান যোগ করে সংখ্যাটির সমকক্ষ দশমিক মান নির্ণয় করা যায়। বাইনারি সংখ্যা হতে দশমিক সংখ্যায় রূপান্তর করতে হলে বাইনারি সংখ্যাটির প্রত্যেকটি বিট কে 2n দ্বারা গুণ করতে হয়, যেখানে n হলো সংখ্যাটির বিটগুলোর অবস্থান, যা ০ থেকে শুরু হয়ে ১, ২, ৩ ইত্যাদি ক্রমে বাড়তে থাকবে এবং ডান দিক হতে শুরু হবে। এবার গুণফলগুলোকে যোগ করে সংখ্যাটির দশমিক মান পাওয়া যায়।
উদাহরণ-১: (১১০১১.১০১)২ বাইনারি থেকে দশমিকে রূপান্তর করুন।
পুর্ণ অংশ: \[ ১ \times ২^৪ + ১ \times ২^৩ + ০ \times ২^২ + ১ \times ২^১ + ১ \times ২^০ \] \[ = ১ \times ১৬ + ১ \times ৮ + ০ \times ৪ + ১ \times ২ + ১ \times ১ \] \[ = ১৬ + ৮ + ০ + ২ + ১ = ২৭ \] ভগ্নাংশ অংশ: \[ ১ \times ২^{-১} + ০ \times ২^{-২} + ১ \times ২^{-৩} \] \[ = ১ \times ০.৫ + ০ \times ০.২৫ + ১ \times ০.১২৫ \] \[ = ০.৫ + ০ + ০.১২৫ = ০.৬২৫ \] পুর্ণ অংশ এবং ভগ্নাংশ একত্র করে: \[ ১১০১১.১০১_{২} = ২৭ + ০.৬২৫ = ২৭.৬২৫_{১০} \]
উদাহরণ-২: (১০১১০০)২ কে দশমিক সংখ্যায় রূপান্তর করুন। \[ ১ \times ২^৫ + ০ \times ২^৪ + ১ \times ২^৩ + ১ \times ২^২ + ০ \times ২^১ + ০ \times ২^০ \] \[ = ১ \times ৩২ + ০ \times ১৬ + ১ \times ৮ + ১ \times ৪ + ০ \times ২ + ০ \times ১ \] \[ = ৩২ + ০ + ৮ + ৪ + ০ + ০ = ৪৪ \] \[ ১০১১০০_{২} = ৪৪_{১০} \]
ভগ্নাংশের ক্ষেত্রে বাইনারি হতে দশমিক সংখ্যায় রূপান্তর
ভগ্নাংশের ক্ষেত্রে বাইনারি বিন্দুর পর হতে বাম হতে শুরু করে ডান দিকে-1, -2, -3 ইত্যাদি দ্বারা অবস্থান চিহ্নিত করে নিতে হয়। এরপর প্রত্যেকটি বিটকে 2n দ্বারা গুণ করে গুণফলগুলোকে যোগ করলে দশমিক মান পাওয়া যায়। যেখানে n হলো-1,-2,-3 ইত্যাদি।
উদাহরণ ১: (০.১১১)২ কে দশমিক সংখ্যায় রূপান্তর করুন।
\[ ১ \times ২^{-১} + ১ \times ২^{-২} + ১ \times ২^{-৩} \] \[ = ১ \times ০.৫ + ১ \times ০.২৫ + ১ \times ০.১২৫ \] \[ = ০.৫ + ০.২৫ + ০.১২৫ = ০.৮৭৫ \] \[ ০.১১১_{২} = ০.৮৭৫_{১০} \] উদাহরণ ২: (১০১০১.১১০১)২ কে দশমিক সংখ্যায় রূপান্তর করুন।
পুর্ণ অংশ: \[ ১ \times ২^৪ + ০ \times ২^৩ + ১ \times ২^২ + ০ \times ২^১ + ১ \times ২^০ \] \[ = ১ \times ১৬ + ০ \times ৮ + ১ \times ৪ + ০ \times ২ + ১ \times ১ \] \[ = ১৬ + ০ + ৪ + ০ + ১ = ২১ \] ভগ্নাংশ অংশ: \[ ১ \times ২^{-১} + ১ \times ২^{-২} + ০ \times ২^{-৩} + ১ \times ২^{-৪} \] \[ = ১ \times ০.৫ + ১ \times ০.২৫ + ০ \times ০.১২৫ + ১ \times ০.০৬২৫ \] \[ = ০.৫ + ০.২৫ + ০ + ০.০৬২৫ = ০.৮১২৫ \] পুর্ণ অংশ এবং ভগ্নাংশ একত্র করে \[ ১০১০১.১১০১_{২} = ২১ + ০.৮১২৫ = ২১.৮১২৫_{১০} \]
অক্টাল থেকে দশমিকে রূপান্তর
অক্টাল সংখ্যার প্রতিটি স্থানীয় মান যোগ করে সংখ্যাটির সমকক্ষ দশমিক মান নির্ণয় করা যায়।
উদাহরণ : (১২৩.৫৪০)৮ কে দশমিকে রূপান্তর করুন।
পুর্ণ অংশ: \[ ১ \times ৮^২ + ২ \times ৮^১ + ৩ \times ৮^০ \] \[ = ১ \times ৬৪ + ২ \times ৮ + ৩ \times ১ \] \[ = ৬৪ + ১৬ + ৩ = ৮৩ \] ভগ্নাংশ অংশ: \[ ৫ \times ৮^{-১} + ৪ \times ৮^{-২} + ০ \times ৮^{-৩} \] \[ = ৫ \times ০.১২৫ + ৪ \times ০.০১৫৬২৫ + ০ \times ০.০০১৯৫৩১২৫ \] \[ = ০.৬২৫ + ০.০৬২৫ + ০ = ০.৬৮৭৫ \] পুর্ণ অংশ এবং ভগ্নাংশ একত্র করে \[ ১২৩.৫৪০_{৮} = ৮৩ + ০.৬৮৭৫ = ৮৩.৬৮৭৫_{১০} \]
হেক্সাডেসিমেল থেকে দশমিকে রূপান্তর
হেক্সাডেসিমেল থেকে দশমিকে রূপান্তরে প্রথমে প্রদত্ত সংখ্যার প্রতিটি অংককে উহার নিজস্ব স্থানীয় মান দ্বারা গুণ করতে হবে। পরে ঐ সমস্ত গুণফলকে যোগ করে হেক্সাডেসিমেল সংখ্যাটির সমকক্ষ দশমিক সংখ্যার মান বের করা যায়।
উদাহরণ: (B৫D.৪৮)১৬-কে দশমিকে রূপান্তর করুন।
পুর্ণ অংশ: \[ B \times ১৬^২ + ৫ \times ১৬^১ + D \times ১৬^০ \] \[ = ১১ \times ২৫৬ + ৫ \times ১৬ + ১৩ \times ১ \] \[ = ২৮১৬ + ৮০ + ১৩ = ২৯০৯ \] ভগ্নাংশ অংশ: \[ ৪ \times ১৬^{-১} + ৮ \times ১৬^{-২} \] \[ = ৪ \times ০.০৬২৫ + ৮ \times ০.০০৩৯০৬২৫ \] \[ = ০.২৫ + ০.০৩১২৫ = ০.২৮১২৫ \] পুর্ণ অংশ এবং ভগ্নাংশ একত্র করে \[ B৫D.৪৮_{১৬} = ২৯০৯ + ০.২৮১২৫ = ২৯০৯.২৮১২৫_{১০} \]
বাইনারি, অক্টাল ও হেক্সাডেসিমেল সংখ্যার মধ্যে পারস্পরিক রূপান্তর
অক্টাল থেকে বাইনারিতে রূপান্তর
উদাহরণ: (১২৭)৮ - কে বাইনারিতে রূপান্তর করুন। \[ ১ \to ০০১ \quad ২ \to ০১০ \quad ৭ \to ১১১ \] বাইনারি গ্রুপগুলোকে একত্র করে: \[ ১২৭_৮ = ০০১০১০১১১_২ \] উদাহরণ : (১১১১০১১)২ - কে অক্টালে রূপান্তর করুন।
পূর্ণাংশের ক্ষেত্রে ডান দিক থেকে প্রতি তিনটি বিট একত্রে নিয়ে ছোট ছোট ভাগ করে বাম দিকে যেতে হবে এবং বাম দিকের ভাগে খালি থাকলে প্রয়োজনীয় ০ দিয়ে পূর্ণ করতে হবে। কিন্তু ভগ্নাংশের ক্ষেত্রে বাইনারি বিন্দুর ডান থেকে তিনটি বিট নিয়ে ছোট ছোট ভাগ করা ভাগে খালি জায়গা থাকলে ডানে প্রয়োজনীয় ০ দিয়ে পূর্ণ করতে হবে।
\[ ০০১ \quad ১১১ \quad ০১১ \] \[ ০০১ \to ১ \quad ১১১ \to ৭ \quad ০১১ \to ৩ \] \[ ১১১১০১১_২ = ১৭৩_৮ \]
হেক্সাডেসিমেল থেকে বাইনারি রূপান্তর
উদাহরণ: (১২A)১৬ - কে অক্টালে রূপান্তর করুন।
\[ ১ \to ০০০১ \quad ২ \to ০০১০ \quad A \to ১০১০ \] \[ ১২A_{১৬} = ০০০১০০১০১০১০_২ \] বাইনারি থেকে হেক্সাডেসিমেলে রূপান্তর \[ ০০১১ \quad ১১১ \] \[ ০০১১ \quad ০১১১ \] \[ ০০১১ \to ৩ \quad ০১১১ \to B \] \[ ১১১১০১১_২ = ৩B_{১৬} \]
অক্টাল-হেক্সাডেসিমেল রূপান্তর
অক্টাল-হেক্সাডেসিমেল সংখ্যা পদ্ধতির পারস্পরিক রূপান্তরের ক্ষেত্রে প্রথমে সংখ্যাটিকে দশমিকে অথবা বাইনারিতে রূপান্তর করে তারপর কাঙ্ক্ষিত সংখ্যা পদ্ধতিতে রূপান্তর করা হয়। এ দুটি পদ্ধতির মধ্যে বাইনারি পদ্ধতির মধ্যস্থতায় রূপান্তরই সহজতম পদ্ধতি।
উদাহরণ: (১২A)১৬ কে অক্টালে রূপান্তর করুন। \[ ১ \to ০০০১ \quad ২ \to ০০১০ \quad A \to ১০১০ \] \[ ১২A_{১৬} = ০০০১০০১০১০_২ \] \[ ০০০ \quad ১০০ \quad ১০_২ \] \[ ০০০ \quad ১০০ \quad ১০০ \] \[ ০০০ \to ০ \quad ১০০ \to ৪ \quad ১০০ \to ২ \] \[ ১২A_{১৬} = ০৪২_{৮} \]
বাইনারি গণিত
দশমিক সংখ্যা পদ্ধতির গাণিতিক প্রক্রিয়াসমূহ (যেমন- যোগ, বিয়োগ, গুণ, ভাগ) বহুল পরিচিত। এ ধরনের গাণিতিক প্রক্রিয়াসমূহ বাইনারি সংখ্যা পদ্ধতিতেও বর্তমান। বাইনারি পদ্ধতিতে গাণিতিক কাজ করা বেশ সহজ কারণ, এক্ষেত্রে মাত্র দুটি সংখ্যা ০ এবং ১ জড়িত থাকে। নিম্নে বাইনারি যোগ, বিয়োগ, গুণ এবং ভাগ পদ্ধতি নিয়ে আলোচনা করা হলো-
বাইনারি গণিত
দশমিক সংখ্যা পদ্ধতির গাণিতিক প্রক্রিয়াসমূহ (যেমন- যোগ, বিয়োগ, গুণ, ভাগ) বহুল পরিচিত। এ ধরনের গাণিতিক প্রক্রিয়াসমূহ বাইনারি সংখ্যা পদ্ধতিতেও বর্তমান। বাইনারি পদ্ধতিতে গাণিতিক কাজ করা বেশ সহজ কারণ, এক্ষেত্রে মাত্র দুটি সংখ্যা ০ এবং ১ জড়িত থাকে। নিম্নে বাইনারি যোগ, বিয়োগ, গুণ এবং ভাগ পদ্ধতি নিয়ে আলোচনা করা হলো-
বাইনারি যোগ
দশমিক পদ্ধতির মতো একই উপায়ে বাইনারি যোগ করা হয়। দুটি বাইনারি অংক যোগের চারটি নিম্নরূপ অবস্থা হয়- \[ ০ + ০ = ০ \] \[ ০ + ১ = ১ \] \[ ১ + ০ = ১ \] \[ ১ + ১ = ০ \quad \text{carry ১} \]
উদাহরণ: (১১০০১০১)২ এর সাথে (১০১০১০১)২ যোগ করুন।
\[ \begin{array}{cccccccc} & ১ & ১ & ০ & ০ & ১ & ০ & ১ \\ + & ১ & ০ & ১ & ০ & ১ & ০ & ১ \\ \hline \end{array} \] \[ ১ + ১ = ০ \quad \text{(carry ১)} \] \[ ০ + ০ + ১ = ১ \quad \text{(carry ০)} \] \[ ১ + ১ = ০ \quad \text{(carry ১)} \] \[ ০ + ০ + ১ = ১ \quad \text{(carry ০)} \] \[ ০ + ১ = ১ \quad \text{(carry ০)} \] \[ ১ + ০ = ১ \quad \text{(carry ০)} \] \[ ১ + ১ = ০ \quad \text{(carry ১)} \] \[ \begin{array}{cccccccc} & ১ & ১ & ০ & ০ & ১ & ০ & ১ \\ + & ১ & ০ & ১ & ০ & ১ & ০ & ১ \\ \hline ১ & 0 & ১ & ১ & ১ & ০ & ১ & ০ \\ \end{array} \] \[ \text{Sum} = ১০১১১০১০_২ \]
(৯F.C৬)১৬ ও (২৭৭.৩৬)৮ যোগ করুন এবং ফলাফল হেক্সাডেসিমেলে প্রকাশ করুন।
\[ ৯ \to ১০০১ \quad F \to ১১১১ \quad C \to ১১০০ \quad ৬ \to ০১১০ \] \[ ৯F.C৬_{১৬} = ১০০১১১১১.১১০০০১১০_{২} \] \[ ২ \to ০১০ \quad ৭ \to ১১১ \quad ৩ \to ০১১ \quad ৬ \to ১১০ \] \[ ২৭৭.৩৬_{৮} = ০১০১১১১১১.০১১১১০_{২} \] \[ \begin{array}{cccccccccc} & ০ & ১ & ০ & ০ & ১ & ১ & ১ & ১ & ১ & . & ১ & ১ & ০ & ০ & ০ & ১ & ১ & ০ \\ + & ০ & ১ & ০ & ১ & ১ & ১ & ১ & ১ & ১ & . & ০ & ১ & ১ & ১ & ১ & ০ & ০ & ০ \\ \hline & ১ & ০ & ১ & ০ & ১ & ১ & ১ & ১ & ১ & . & ০ & ০ & ১ & ১ & ১ & ১ & ১ & ০ \\ & ১ & & ৫ & & & & F & & & . & & ৩ & & & & E & & \\ \end{array} \]
উল্লেখ্য, কম্পিউটারের যাবতীয় গাণিতিক কাজ বাইনারি যোগের মাধ্যমে সম্পন্ন করা হয়। এ কারণেই কম্পিউটার বিজ্ঞানে বাইনারি যোগ খুব গুরুত্বপূর্ণ অপারেশন। গুণ হলো বার বার যোগ করা এবং ভাগ হলো বার বার বিয়োগ করা। আবার ২-এর পরিপূরক পদ্ধতিতে বাইনারি যোগের মাধ্যমেই বিয়োগ করা যায়। কাজেই যোগ করতে পারার মানেই হলো গুণ বিয়োগ মানেই ভাগ করতে পারা।
বাইনারি বিয়োগ
বাইনারি সংখ্যা পদ্ধতিতে বিয়োগের নিয়ম দশমিক পদ্ধতির অনুরূপ। দুটি বাইনারি অংক বিয়োগের জন্য নিম্নোক্ত চারটি অবস্থার সৃষ্টি হয়-
\[ ০ - ০ = ০ \] \[ ১ - ০ = ১ \] \[ ০ - ১ = ১ \quad \text{(carry ১)} \] \[ ১ - ১ = ০ \]
এ পদ্ধতিতেও দশমিক পদ্ধতির মতো ছোট সংখ্যা অর্থাৎ ১ বিয়োগ করলে ধার থাকে ১। এ ধার পরবর্তী স্তম্ভ থেকে নেয়া হয়। কম্পিউটারে এই নিয়মে বিয়োগ করা হয় না। ২ এর পরিপূরক পদ্ধতিতে যোগের সাহায্যে বিয়োগ করা হয়।
বাইনারি গুণ
বাইনারি পদ্ধতিতে খুব সহজে গুণ করা যায়। দশমিক পদ্ধতিতে গুণ করার জন্য নামতা মনে রাখতে হয়। কিন্তু বাইনারি পদ্ধতিতে মাত্র চারটি গুণফল জানলেই যথেষ্ট। তবে কম্পিউটারে এই নিয়মে গুণ করা হয় না। নিচে বাইনারি চারটি অবস্থা দেয়া হলো-
\[ ০ \times ০ = ০ \] \[ ১ \times ০ = ০ \] \[ ০ \times ১ = ০ \] \[ ১ \times ১ = ১ \]
বাইনারি ভাগ
দশমিক পদ্ধতির ভাগের নিয়মেই বাইনারিতে ভাগ করা হয়। এখানে কোনো রকম জটিলতা নেই। বাইনারি পদ্ধতিতে ০ দিয়ে ভাগ করাকে অর্থহীন বলে। এ পদ্ধতিতে ব্যবহৃত চারটি অবস্থা নিম্নরূপ-
\[ \frac{o}{o} = \text{Meaningless} \] \[ \frac{১}{০} = \text{Meaningless} \] \[ \frac{০}{১} = ০ \] \[ \frac{১}{১} = ১ \]
কম্পিউটার কোডিং (Computer Coding)
- কম্পিউটার সিস্টেমে ব্যবহৃত প্রতিটি বর্ণ, সংখ্যা বা বিশেষ চিহ্নকে পৃথক পৃথকভাবে CPU-কে বোঝানোর জন্য ব্যবহৃত অদ্বিতীয় সংকেতকে বলে- কোড (Code)।
- বিভিন্ন প্রকার কোড হলো-অক্টাল কোড (Octal Code), Hexadecimal Code, BCD Code, Alphanumeric Code, ASCII Code, EBCDIC Code, Unicode, Morse Code, Gray Code ইত্যাদি।
- তিন বিট বিশিষ্ট কোডকে বলে- অক্টাল কোড। যেমন- (৪৬)১০ = (১০১১১০)২ = (৫৬)৮ = (১০১ ১১০)২ (অক্টাল কোড)।
- চার বিট বিশিষ্ট কোডকে বলে- হেক্সাডেসিমাল কোড। যেমন (৩৭)১০ = (২৫)১৬ = (০০১০ ০১০১)২ (হেক্সাডেসিমাল কোড)।
- দশমিক সংখ্যাকে বাইনারি সংখ্যায় রূপান্তরের কোডকে বলে- BCD Code।
- বিভিন্ন ইলেকট্রনিক ডিসপ্লে বোর্ডে তারিখ সংরক্ষণে ব্যবহৃত কোড হলো- BCD।
- বিভিন্ন প্রকার BCD Code গুলো হলো- BCD 8421, BCD 7421, BCD 5421, BCD 2421 ইত্যাদি।
- বর্ণ, অংক এবং বিভিন্ন চিহ্নের জন্য ব্যবহৃত কোডকে বলে- Alpha numeric Code।
- কয়েকটি জনপ্রিয় Alpha-numeric Code হলো- ASCII Code, EBCDIC Code, Unicode ইত্যাদি।
- ASCII-এর পূর্ণরূপ হচ্ছে- American Standard Code for Information Interchange।
- ASCII Code ২ প্রকার; যথা- ১. ASCII-7 এবং ২. ASCII-৪।
- বর্তমানে ASCII Code বলতে বোঝানো হয়- ASCII-8 কে।
- ২৫৬টি অদ্বিতীয় চিহ্নকে নির্দিষ্ট করা যায়- ASCII-8 দ্বারা।
- মূলত ভুল নির্ণয়ের জন্য ব্যবহৃত হয়- প্যারিটি বিট।
- আসকি কোড হলো- বহুল পরিচিত ৭ বিট আলফা নিউমেরিক কোড।
- আসকি কোড দ্বারা প্রকাশ করা যায়- ২৭ বা ১২৮টি অদ্বিতীয় অঙ্ক, অক্ষর এবং চিহ্ন।
- BCD শব্দটির পূর্ণরূপ হলো-Binary Coded Decimal।
- BCD কোড ব্যবহৃত হয়- দশমিক পদ্ধতির সংখ্যাকে বাইনারি সংখ্যায় প্রকাশের জন্য।
- BCD কোড গঠিত হয়- ৪টি বিট দিয়ে।
- EBCDIC এর পূর্ণরূপ হলো- Extended Binary Coded Decimal Interchange Code । ■ EBCDIC কোড হলো- আইবিএম কোম্পানি কর্তৃক উদ্ভাবিত ৮টি আলফা নিউমেরিক কোড।
- EBCDIC কোডে প্রকাশ করা যায়- ২৮ বা ২৫৬টি অদ্বিতীয় অঙ্ক, অক্ষর বা চিহ্ন।
- ইউনিকোড (UNICODE) ব্যবহৃত হয় বিশ্বের ছোট বড় সকল ভাষাকে কম্পিউটারে কোডভুক্ত করার জন্য।
- ইউনিকোড হলো- মূলত ২ বাইট বা ১৬ বিটের কোড।
- ইউনিকোডে প্রকাশ করা যায়- ২১৬ বা ৬৫৫৩৬ টি অদ্বিতীয় অঙ্ক, অক্ষর এবং চিহ্ন।
- IBM-360 ও IBM-370 এ ব্যবহৃত কোড ছিল- EBCDIC Code।
- EBCDIC-তে ০ হতে ৯ সংখ্যার জন্য ব্যবহৃত হয়- ১১১১।
- বিশ্বের সকল ভাষাকে কম্পিউটারে কোডভুক্ত করার জন্য তৈরিকৃত কোডকে বলে- ইউনিকোড (Unicode) ।
- Unicode -এর পূর্ণ অর্থ হলো- Universal Code (সর্বজনীন কোড)।
- Unicode হচ্ছে- 16 bit Code।
- বাইনারি ডেটাকে এক স্থান থেকে অন্য স্থানে স্থানান্তরের অতিরিক্ত বিটকে বলে- প্যারিটি বিট।
- ১৯৯১ সালে ইউনিকোড উদ্ভাবন করেন- Apple Corporation Xerox Corporation যৌথভাবে।
- বাংলা ভাষা ইউনিকোডযুক্ত হয়েছে- Unicode Consortium-এর সদস্য হয়ে।
ডিজিটাল লজিক (Digital Logic)
বুলিয়ান অ্যালজেবরা (Boolean Algebra)
- ইংরেজ গণিতজ্ঞ জর্জ বুলি (George Boole) সর্বপ্রথম বুলিয়ান অ্যালজেবরা নিয়ে আলোচনা করেন- ১৮৪৭ সালে।
- বুলিয়ান অ্যালজেবরা মূলত তৈরি হয়েছে- লজিকের সত্য এবং মিথ্যা এই দুই স্তরের উপর ভিত্তি করে।
- কম্পিউটারের সমস্ত গাণিতিক ও যুক্তিমূলক সমস্যা সমাধান করা হয়- বুলিয়ান অ্যালজেবরার সাহায্যে।
- বুলিয়ান অ্যালজেবরায় সমস্ত কাজ করা হয়- শুধুমাত্র বুলিয়ান যোগ এবং গুণ এর সাহায্যে।
বুলিয়ান স্বতঃসিদ্ধ (Postulates)
বুলিয়ান অ্যালজেবরা যোগের ক্ষেত্রে যে সব নিয়ম মেনে চলে সেগুলো নিম্নরূপ: \[ 0 + 0 = 0 \] \[ 0 + 1 = 1 \] \[ 1 + 0 = 1 \] \[ 1 + 1 = 1 \] বুলিয়ান অ্যালজেবরা গুণের ক্ষেত্রে যে সব নিয়ম মেনে চলে সেগুলো নিম্নরূপ: \[ 0 \cdot 0 = o \] \[ 0 \cdot 1 = 0 \] \[ 1 \cdot 0 = 0 \] \[ 1 \cdot 1 = 1 \]
বুলিয়ান উপপাদ্য (Boolean Theorems)
বুলিয়ান অ্যালজেবরার সাধারণ উপপাদ্যগুলো নিচে দেয়া হলো। এই সকল উপপাদ্য বুলিয়ান স্বতঃসিদ্ধেরই আরেকরূপ। এই সকল উপপাদ্যের সাহায্যে জটিল সমীকরণ সমধান করা হয়।
মৌলিক উপপাদ্য \[ A + 0 = A \] \[ A \cdot 1 = A \] \[ A + \overline{A} = 1 \] \[ A \cdot \overline{A} = 0 \] \[ A + A = A \] \[ A \cdot A = A \] \[ A + 1 = 1 \] \[ A \cdot 0 = 0 \] বিনিময় উপপাদ্য \[ A + \overline{B} = \overline{B} + A \] \[ A \cdot \overline{B} = \overline{B} \cdot A \] অনুষঙ্গ উপপাদ্য \[ A + (B + C) = (A + B) + C \] \[ A \cdot (B \cdot C) = (A \cdot B) \cdot C \] বিভাজন উপপাদ্য \[ A \cdot (B + C) = A \cdot B + A \cdot C \] \[ A + B \cdot C = (A + B)(A + C) \] ডি-মরগ্যানের উপপাদ্য \[ \overline{A + B} = \overline{A} \cdot \overline{B} \] \[ \overline{A \cdot B} = \overline{A} + \overline{B} \] সহায়ক উপপাদ্য \[ A + A \cdot B = A \] \[ \overline{\overline{A}} = A \] \[ A \cdot (A + B) = A \]
লজিক গেইট (Logic Gate)
- যে সকল ডিজিটাল ইলেক্ট্রনিক সার্কিট যুক্তিভিত্তিক সংকেতের প্রবাহ নিয়ন্ত্রণ করে সে সকল সার্কিটকে বলে লজিক গেইট। । ডিজিটাল ইলেক্ট্রনিক্সে তিনটি মৌলিক লজিক গেইট ব্যবহার হয়। যথা-
- অর (OR) গেইট
- অ্যান্ড (AND) গেইট
- নট (NOT) গেইট
- ডিজিটাল সিস্টেমে বাইনারি ০ বা ১ প্রকৃতপক্ষে ০ বা ১ ভোল্টেজকে- প্রকাশ করে না।
- ভোল্টেজ লেবেল থেকে ০.৮ ভোল্টেজ হলে লজিক ০ এবং ভোল্টেজ লেবেল ২ থেকে ৫ ভোল্ট হয় তাকে লজিক ১ ধরা হয়।
অর (OR) গেইট
অর গেইটে দুই বা দুই-এর অধিক ইনপুট এবং একটি আউটপুট থাকে। অর গেইটের যে কোনো একটি ইনপুট ১ হলে আউটপুট ১ হবে।

| Input | Output | |
|---|---|---|
| A | B | A OR B |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
অ্যান্ড (AND) গেইট
অ্যান্ড গেইটে দুই বা দুইয়ের অধিক ইনপুট এবং একটি আউটপুট থাকে। অ্যান্ড গেইটের সকল ইনপুট ১ হলেই কেবলমাত্র আউটপুট ১ হবে অন্যথায় আউটপুট ০ হবে।

| Input | Output | |
|---|---|---|
| A | B | A OR B |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
নট (NOT) গেইট
নট গেইটে একটি ইনপুট ও একটি আউটপুট থাকে। নট গেইটের ইনপুট ১ হলে আউটপুট ০ এবং ইনপুট ০ হলে আউটপুট ১ হয়।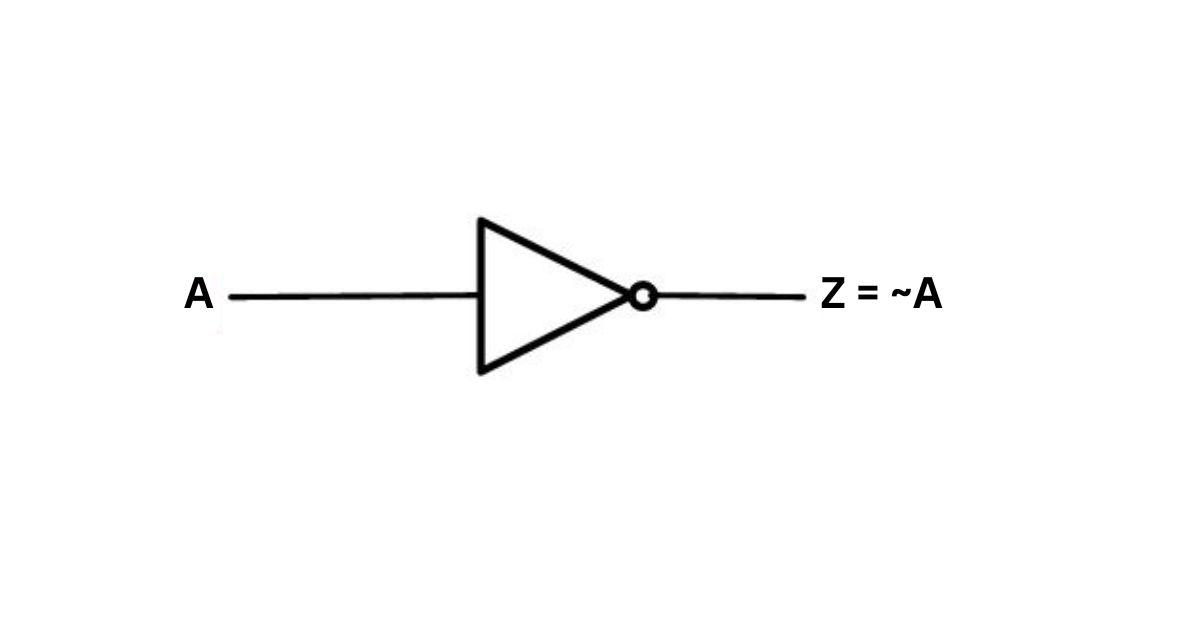
Input
| Input | Output |
|---|---|
| A | NOT A |
| 1 | 0 |
| 0 | 1 |
ডিজিটাল ইলেক্ট্রনিক্সে উপরোক্ত মৌলিক তিনটি লজিক গেইট ছাড়া আরও কিছু গেইট ব্যবহার করা হয়। যথা- ন্যান্ড গেইট, নর গেইট, এক্স অর গেইট, এক্স নর গেইট। এই গেইটগুলো মৌলিক গেইট দ্বারা তৈরি করা যায়।
ন্যান্ড (NAND) গেইট
অ্যান্ড গেইট হতে নির্গত সংকেতটি নট গেইটের মধ্য দিয়ে প্রবাহিত করলে ন্যান্ড (NAND) গেইটের কাজ হয়। অর্থাৎ অ্যান্ডের পর নট যুক্ত করে ন্যান্ড গেইট বাস্তবায়ন করা হয়। লজিক সার্কিট তৈরির জন্য ন্যান্ড গেইটের বহুল প্রচলন রয়েছে।
| Input | Output | |
|---|---|---|
| A | B | A OR B |
| 0 | 0 | 1 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 0 |
নর (NOR) গেইট
অর গেইটের পর নট গেইট থাকলে তাদের সংযুক্ত ফল নর (NOR) গেইটের কাজ করে।
| Input | Output | |
|---|---|---|
| A | B | A OR B |
| 0 | 0 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 1 | 0 |
এক্স-অর (XOR) গেইট
মৌলিক গেইট দিয়ে এই সার্কিট তৈরি করা গেলেও অ্যান্ড, অর, নট, ন্যান্ড ও নর গেইটের মতো এটি একীভূত সার্কিট আকারে পাওয়া যায়।
| Input | Output | |
|---|---|---|
| A | B | A OR B |
| 0 | 0 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 1 | 1 |
এক্স-নর (X-NOR) গেইট
এক্স-অর গেইটের আউটপুটকে নট গেইট দিয়ে প্রবাহিত করলে এক্স-নর গেইট পাওয়া যায়।
| Input | Output | |
|---|---|---|
| A | B | A OR B |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
- বাইনারী সংখ্যার-১ এর পরিপূরক বা 1's compliment বলতে-ঐ সংখ্যার-1 এর স্থলে 0 এবং 0 স্থলে 1 দ্বারা প্রতিস্থাপন বোঝায়।
- 100110-এর 1's compliment-011001
- বাইনারী সংখ্যাকে 1-এর পরিপূরক করে তার সাথে 1 যোগ করলে ২-এর পরিপূরক বা 2's compliment পাওয়া যায়।
- ২ এর পরিপূরকের সাহায্যে শুধু যোগের মাধ্যমে যোগ, বিয়োগ, গুণ ও ভাগের কাজ করা সম্ভব।
- অ্যাডার - ডিজিটাল ইলেকট্রনিক্সে যে সমবায় সার্কিট দ্বারা যোগ করা হয়।
- অ্যাডার দুই ধরনের, যথা: হাফ অ্যাডার ও ফুল অ্যাডার
- হাফ অ্যাডার - দুটো বিট যোগ করলে যোগফল ও হাতে থাকা সংখ্যা বা ক্যারি বের করতে পারে।
- ফুল অ্যাডার হলো এমন একটি সমবায় সার্কিট যা একটি ক্যারি ও দুটি সংখ্যা বিটসহ মোট তিনটি বিট যোগ করে যোগফল ও হাতে থাকা সংখ্যা ও ক্যারি বের করতে পারে। দুটো হাফ অ্যাডার দ্বারা একটি ফুল অ্যাডারের কাজ করা যায়।
- এনকোডার হলো - এক ধরনের সমবায় লজিক সার্কিট যা কোনো ডেটা, সিগন্যাল বা সংকেতকে ডিজিটাল সিস্টেমে বোধগম্য কাঙ্খিত কোনো কোডে পরিবর্তন করে। এর দ্বারা সর্বাধিক 2n টি ইনপুট থেকে n টি আউটপুট লাইনে আউটপুট পাওয়া যায়।
- ডিকোডার হলো - এক ধরনের সমবায় ডিজিটাল সার্কিট যার সাহায্যে n টি ইনপুট থেকে সর্বাধিক 2n টি আউটপুট লাইনের একটিতে 1 ও বাকি সবকটিতে আউটপুট পাওয়া যায়।
- ফ্রিপ-ফ্লপ হলো - লজিক গেইট দ্বারা তৈরি এক ধরনের মেমরি উপাদান যা একটি বাইনারী বিট সংরক্ষণ করতে পারে। ফ্লিপ-ফ্লপের দুটি স্থায়ী অবস্থা (০, ১) আছে এবং উহা দুটি স্থায়ী অবস্থার যে কোনো একটিতে থাকতে পারে।
- রেজিস্টার হলো- একগুচ্ছ ফ্রিপ-ফ্লপ যার প্রত্যেকটি এক বিট তথ্য সংরক্ষণ করতে পারে। একটি n-bit রেজিস্টারে n-সংখ্যক ফ্লিপ-ফ্লপ থাকে যা বাইনারী n-bit তথ্য সংরক্ষণ করতে পারে।
- কাউন্টার হলো- এমন একটি সিকুয়েন্সিয়াল সার্কিট যা তাতে প্রদানকৃত ইনপুট পালসের সংখ্যা গুণতে পারে।
- মডিউলাস কাউন্টার সর্বাধিক যতটি সংখ্যা গুণতে পারে।
- কোনো কাউন্টারে n টি ফ্রিপ-ফ্লপ থাকলে তার মডিউলাস সংখ্যা- 2n